• 栈
  • 定义和基础理论
  • 基础操作
    • 初始化
    • 入栈
    • 出栈
    • 取栈顶元素
• 队列
  • 定义和基础理论
  • 基础操作
    • 初始化
    • 求队列长度
    • 入队
    • 出队
    • 取队头元素
  • 双向队列
• 小结

栈

定义和基础理论

栈是一种限制插入和删除操作只能在一个位置进行的列表，栈遵循后进先出（LIFO—Last In First Out）的原则，在栈中，每当新元素被添加，它就被放置在栈顶。当元素被移除时，栈顶的元素被取出

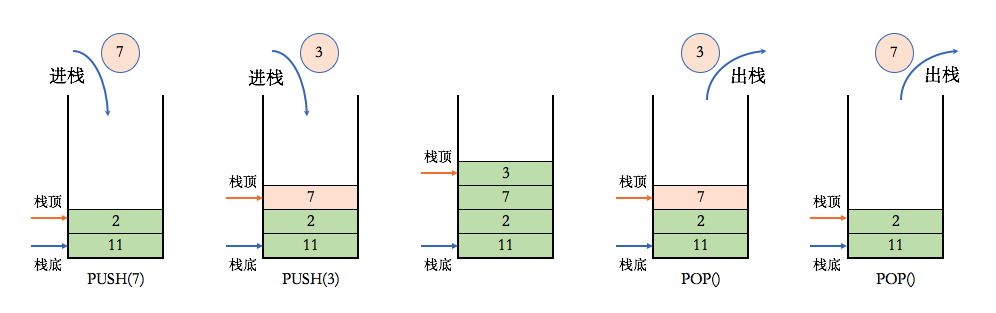
以下是常用的应用场景

• 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以回到原来的程序中
• 递归的调用：可以用来在函数调用的时候存储断点，储存下一个指令的地址外，也将参数、区域变量等数据存入栈中
• 表达式的转换[中缀表达式转后缀表达式]与求值
• 二叉树的遍历
• 图形的深度优先搜索法

定义分为两种栈的定义，一种是顺序栈，一种是链栈

#define MAXSIZE 100
typedef struct
{
	SElemType *base;
	SElemType *top;
	int stacksize;
}SqStack;

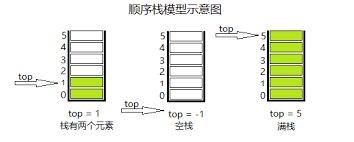
base为栈底指针，初始化完成后，栈底指针base始终指向栈底的位置，若base的值为NULL，则表明栈结构不存在。top为栈顶指针，甚初值指向栈底。每当插入新的栈顶元素时，指针top增1；删除栈顶元素时，指针top减1。因此，栈空时，top和base的值相等，都指向栈底；栈非空时，top始终指向栈顶元素的上一个位置；stacksize 指示栈可使用的最大容量，后面算法3.1的初始化操作为顺序栈动态分配MAXSIZE大小的数组空间，将stacksize置为MAXSIZE

typedef struct StackNode
{
	ElemType data;
	struct StackNode *next;
}StackNode, *LinkStack;

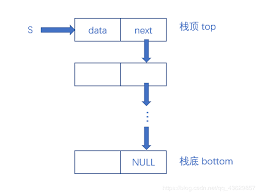
链栈一般选用单链表来表示；由于栈的主要操作是在栈顶插入删除，显然以链表头部是最方便的，因为在链表那节讲过，链表插入时间消耗在找点上，如果是第一个就不需要消耗大量时间，当然，我们为了操作方便一般不需要设置头结点

基础操作

初始化

顺序栈的初始化是为顺序栈动态分配一个预定义大小的数组空间

Status InitStack(SqStack &S)
{
	S.base = new SElemType[MAXSIZE];
	if (!S.base) exit (OVERFLOW);
	S.top = S.base;
	S.stacksize = MAXSIZE;
	return OK;
}

链栈初始化操作是构造一个空栈，因为没有头结点，所以直接将栈顶指针置空即可

Status InitStack(LinkStack &S)
{
	S = NULL;	
	return OK;
}

入栈

出栈对于两种栈来说并没有需要额外注意的，都是在栈顶插入一个新的元素

Status Push(SqStack &S, SElemType e)
{
	if (S.top - S.base == S.stacksize) return ERROR;
	*S.top++ = e;
	return OK;
}

Status Push(LinkStack &S, SElemType e)
{
	p = new StackNode;
	p->data = e;
	p->next = S;
	S = q;
	return OK;
}

出栈

出栈就是将栈顶元素删除，两者有所不同主要存在与资源的释放

Status Pop(SqStack &S, SElemType &e)
{
	if (S.top == S.base) return ERROR;
	e = *--S.top;
	return OK;
}

Status Pop(LinkStack &S, SElemType &e)
{
	if (S == NULL) return ERROR;
	e = S->data;
	p = S;
	S = S->next;
	delete p;
	return OK;
}

取栈顶元素

栈非空的时候，此操作返回当前栈顶元素的值，栈顶指针保证不变

SElemType GetTop()
{
	if (S.top != S.base)
		return *(S.top - 1);
}

SElemType GetTop()
{
	if (S != NULL)
		return S->data;
}

队列

定义和基础理论

队列的操作跟栈的操作类似，不同的是，删除是在表的头部(即队头进行)；队列遵循的是后进先出（FIFO—First In First Out）

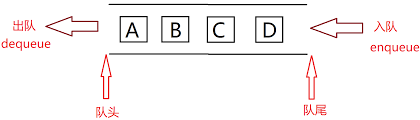
队列也有两种存储表示，顺序表示和链式表示；、

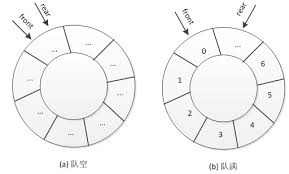
但是当我们使用顺序存储的时候，常会因在最大空间的位置插入新的队尾元素导致数组越界，但实际可用空间并未占满，这种现象被称为”假溢出”；为解决这个问题，把顺序队列变为了一个环状的空间，被称为循环队列；但同时也会引出一个问题，如何区别队列空满的情况，有两种处理情况，一种是少用一个元素空间，队空的条件是Q.front == Q.rear，队满的条件(Q.rear + 1) % MAXQSIZE == Q.front，另外一种是设置一个标志位区别

#define MAXQSIZE 100
typedef struct 
{
	QElemType *base;
	int front;
	int rear;
}sqQueue;

链队基本和链栈一样，只不过为了操作方便会给链队添加一个头结点

typedef struct QNode
{
	QElemType data;
	struct QNode *next;
}QNode, *QueuePtr;
typedef struct
{
	QueuePtr front;
	QueuePtr rear;
}LinkQueue;

基础操作

初始化

循环队列的初始化就是动态分配一个预定义大小为MAXQSIZE的数组空间

Status InitQueue(SqQueue &Q)
{
	Q.base = new QElemType[MAXQSIZE];
	if (!Q.base) exit (OVERFLOW);
	Q.front = Q.rear;
	Q.rear = 0;
	return OK;
}

链队初始化操作是构造一个只有头结点的空队

Status InitQueue(LinkQueue &Q)
{
	Q.front = Q.rear = new QNode;
	Q.front->next = NULL;
	return OK;
}

求队列长度

对于非循环队列，尾指针和头指针的差值就是队列长度，但对于循环队列，差值可能为负数，所以最后插值还需要加MAXQSIZE，在求余

int QueueLength (SqQueue Q)
{
	return (Q.rear - Q.front + MAXQSIZE) % MAXQSIZE;
}

入队

入队是在队尾插入一个新的元素

Status EnQueue (SqQueue &Q, QElemType e)
{
	if ((Q.rear + 1) % MAXQSIZE == Q.front) return ERROR;
	Q.base[Q.rear] = e;
	Q.rear = (Q.rear + 1) % MAXQSIZE;
	return OK;
}

和循环队列不同的是，链队在入队之前不需要判断是否满，需要为入队元素动态分配一个空间

Status EnQueue (LinkQueue &Q, QElemType e)
{
	p = new QNode;
	p->data = e;
	p->next = NULL;
	Q.rear->next = p;
	Q.rear = p;
	return OK;
}

出队

出队操作是将队头元素删除

Status DeQueue (SqQueue &Q, QElemType &e)
{
	if (Q.front == Q.rear) return ERROR;
	e = Q.base[Q.front];
	Q.front = (Q.front + 1) % MAXQSIZE;
	return OK;
}

和入队类似，我们并不需要判断队列是否为空，不同的是，链队在出队后需要释放队头元素所占的空间；需要注意的是出队操作的时候还需要考虑当队列最后一个元素被删除后，队列尾指针也丢失了，因此需要对队尾指针重新赋值

Status DeQueue (LinkQueue &Q, QElemType &e)
{
	if(Q.front == Q.rear) return ERROR;
	p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	if (Q.rear == p) Q.rear = Q.front;
	delete p;
	return OK;
}

取队头元素

当队列非空的时候，取出头元素会返回头元素的值，队头指针保持不变

QElemType GetHead (SqQueue Q)
{
	if (Q.front != Q.rear) return Q.base[Q.front];
}

QElemType GetHead(LinkQueue Q)
{
	if (Q.front != Q.rear) return Q.front->next->data;
}

双向队列

在队列中，我们仅能删除头部元素或在尾部添加元素；双向队列（double-ended queue）提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作

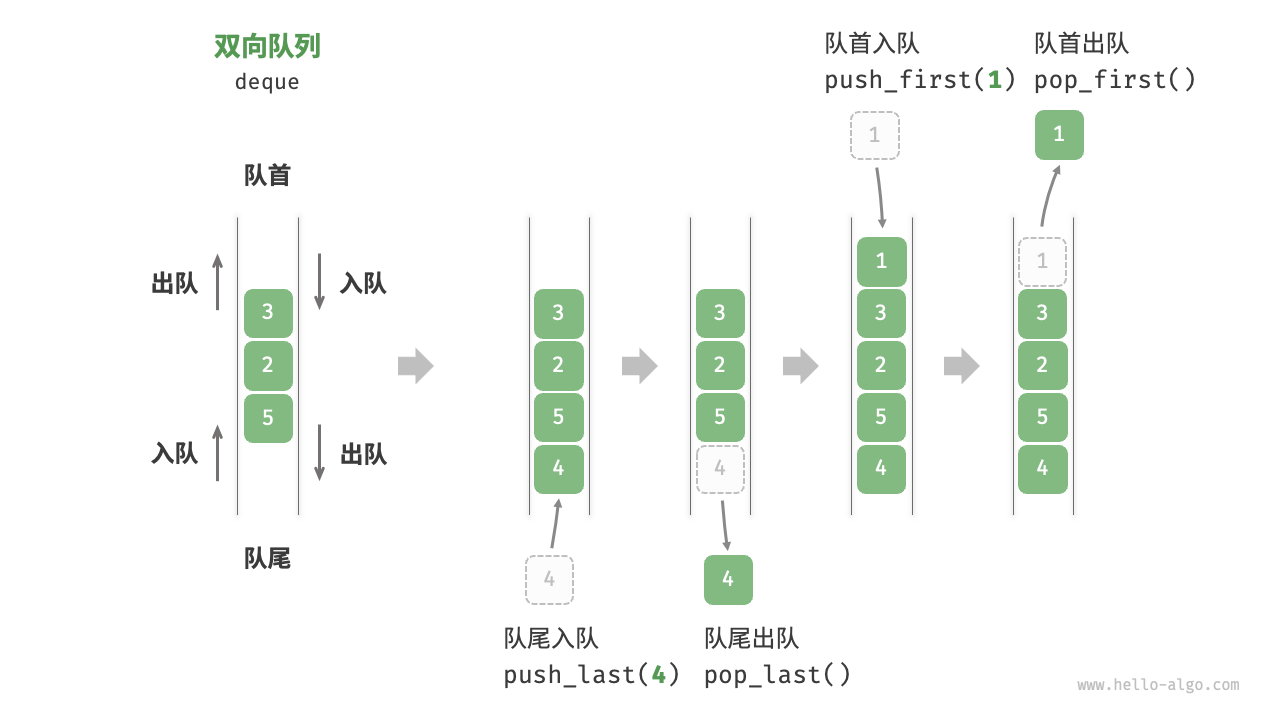
双向队列的实现与队列类似，可以选择链表或数组作为底层数据结构

小结

• 浏览器的前进后退功能本质上是“栈”的体现。当用户访问一个新页面时，该页面会被添加到栈顶；当用户点击后退按钮时，该页面会从栈顶弹出
• 撤销（undo）和反撤销（redo）的实现：使用两个栈，栈 A 用于撤销，栈 B 用于反撤销。 每当用户执行一个操作，将这个操作压入栈 A ，并清空栈 B 。 当用户执行“撤销”时，从栈 A 中弹出最近的操作，并将其压入栈 B 。 当用户执行“反撤销”时，从栈 B 中弹出最近的操作，并将其压入栈 A